Parameterized inference from multidimensional data
Kyle Cranmer, Juan Pavez, Gilles Louppe, March 2016.
For the sake of the illustration, we will assume 5-dimensional feature $\mathbf{x}$ generated from the following process $p_0$:
-
$\mathbf{z} := (z_0, z_1, z_2, z_3, z_4)$, such that $z_0 \sim {\cal N}(\mu=\alpha, \sigma=1)$, $z_1 \sim {\cal N}(\mu=\beta, \sigma=3)$, $z_2 \sim {\text{Mixture}}(\frac{1}{2}\,{\cal N}(\mu=-2, \sigma=1), \frac{1}{2}\,{\cal N}(\mu=2, \sigma=0.5))$, $z_3 \sim {\text{Exponential}(\lambda=3)}$, and $z_4 \sim {\text{Exponential}(\lambda=0.5)}$;
-
$\mathbf{x} := R \mathbf{z}$, where $R$ is a fixed semi-positive definite $5 \times 5$ matrix defining a fixed projection of $\mathbf{z}$ into the observed space.
%matplotlib inline import matplotlib.pyplot as plt plt.set_cmap("viridis") import numpy as np import theano from scipy.stats import chi2
from carl.distributions import Join from carl.distributions import Mixture from carl.distributions import Normal from carl.distributions import Exponential from carl.distributions import LinearTransform from sklearn.datasets import make_sparse_spd_matrix # Parameters true_A = 1. true_B = -1. A = theano.shared(true_A, name="A") B = theano.shared(true_B, name="B") # Build simulator R = make_sparse_spd_matrix(5, alpha=0.5, random_state=7) p0 = LinearTransform(Join(components=[ Normal(mu=A, sigma=1), Normal(mu=B, sigma=3), Mixture(components=[Normal(mu=-2, sigma=1), Normal(mu=2, sigma=0.5)]), Exponential(inverse_scale=3.0), Exponential(inverse_scale=0.5)]), R) # Define p1 at fixed arbitrary value theta1 := 0,0 p1 = LinearTransform(Join(components=[ Normal(mu=0, sigma=1), Normal(mu=0, sigma=3), Mixture(components=[Normal(mu=-2, sigma=1), Normal(mu=2, sigma=0.5)]), Exponential(inverse_scale=3.0), Exponential(inverse_scale=0.5)]), R) # Draw data X_true = p0.rvs(500, random_state=314)
# Projection operator print(R)
[[ 1.31229955 0.10499961 0.48310515 -0.3249938 -0.26387927] [ 0.10499961 1.15833058 -0.55865473 0.25275522 -0.39790775] [ 0.48310515 -0.55865473 2.25874579 -0.52087938 -0.39271231] [-0.3249938 0.25275522 -0.52087938 1.4034925 -0.63521059] [-0.26387927 -0.39790775 -0.39271231 -0.63521059 1. ]]
# Plot the data import corner fig = corner.corner(X_true, bins=20, smooth=0.85, labels=["X0", "X1", "X2", "X3", "X4"]) #plt.savefig("fig3.pdf")
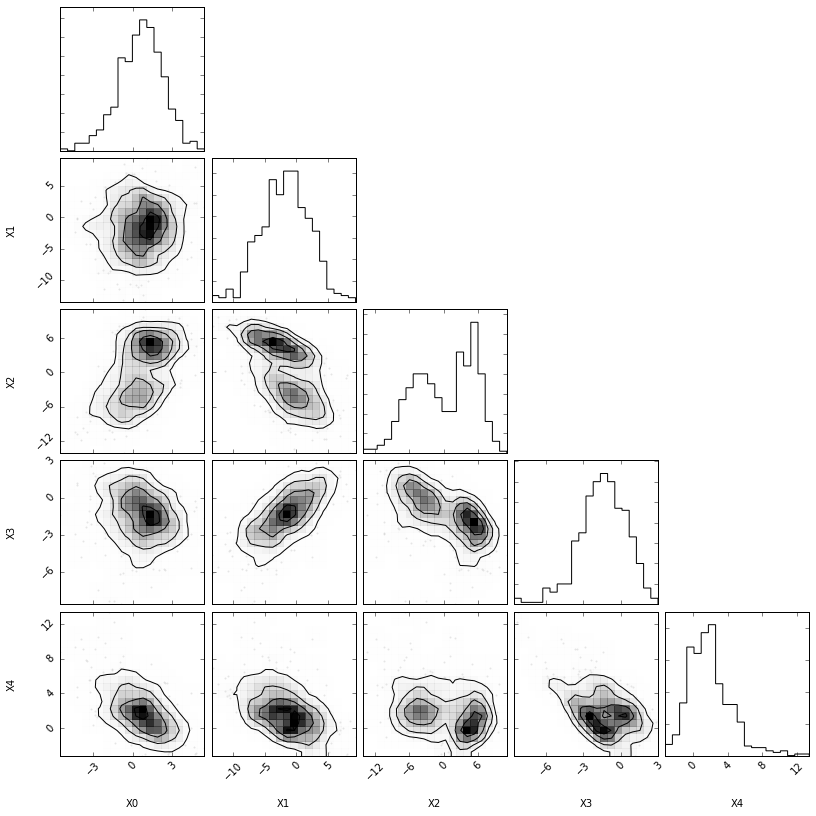
Exact likelihood setup
# Minimize the exact LR from scipy.optimize import minimize def nll_exact(theta, X): A.set_value(theta[0]) B.set_value(theta[1]) return (p0.nll(X) - p1.nll(X)).sum() r = minimize(nll_exact, x0=[0, 0], args=(X_true,)) exact_MLE = r.x print("Exact MLE =", exact_MLE)
Exact MLE = [ 1.01185168 -0.92213112]
# Exact contours A.set_value(true_A) B.set_value(true_B) bounds = [(exact_MLE[0] - 0.16, exact_MLE[0] + 0.16), (exact_MLE[1] - 0.5, exact_MLE[1] + 0.5)] As = np.linspace(*bounds[0], 100) Bs = np.linspace(*bounds[1], 100) AA, BB = np.meshgrid(As, Bs) X = np.hstack((AA.reshape(-1, 1), BB.reshape(-1, 1))) exact_contours = np.zeros(len(X)) i = 0 for a in As: for b in Bs: exact_contours[i] = nll_exact([a, b], X_true) i += 1 exact_contours = 2. * (exact_contours - r.fun)
plt.contour(As, Bs, exact_contours.reshape(AA.shape).T, levels=[chi2.ppf(0.683, df=2), chi2.ppf(0.9545, df=2), chi2.ppf(0.9973, df=2)], colors=["w"]) plt.contourf(As, Bs, exact_contours.reshape(AA.shape).T, 50, vmin=0, vmax=30) cb = plt.colorbar() plt.plot([true_A], [true_B], "r.", markersize=8) plt.plot([exact_MLE[0]], [exact_MLE[1]], "g.", markersize=8) #plt.plot([gp_MLE[0]], [gp_MLE[1]], "b.", markersize=8) plt.axis((*bounds[0], *bounds[1])) plt.xlabel(r"$\alpha$") plt.ylabel(r"$\beta$") #plt.savefig("fig4a.pdf") plt.show()
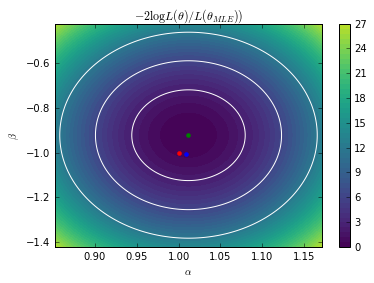
Likelihood-free setup
In this example we will build a parametrized classifier $s(x; \theta_0, \theta_1)$ with $\theta_1$ fixed to $(\alpha=0, \beta=0)$.
# Build classification data from carl.learning import make_parameterized_classification bounds = [(-3, 3), (-3, 3)] X, y = make_parameterized_classification( p0, p1, 1000000, [(A, np.linspace(*bounds[0], num=30)), (B, np.linspace(*bounds[1], num=30))], random_state=1)
# Train parameterized classifier from carl.learning import as_classifier from carl.learning import make_parameterized_classification from carl.learning import ParameterizedClassifier from sklearn.neural_network import MLPRegressor from sklearn.pipeline import make_pipeline from sklearn.preprocessing import StandardScaler from sklearn.model_selection import RandomizedSearchCV clf = ParameterizedClassifier( make_pipeline(StandardScaler(), as_classifier(MLPRegressor(learning_rate="adaptive", hidden_layer_sizes=(40, 40), tol=1e-6, random_state=0))), [A, B]) clf.fit(X, y)
For the scans and Bayesian optimization we construct two helper functions.
from carl.learning import CalibratedClassifierCV from carl.ratios import ClassifierRatio def vectorize(func): def wrapper(X): v = np.zeros(len(X)) for i, x_i in enumerate(X): v[i] = func(x_i) return v.reshape(-1, 1) return wrapper def objective(theta, random_state=0): print(theta) # Set parameter values A.set_value(theta[0]) B.set_value(theta[1]) # Fit ratio ratio = ClassifierRatio(CalibratedClassifierCV( base_estimator=clf, cv="prefit", # keep the pre-trained classifier method="histogram", bins=50)) X0 = p0.rvs(n_samples=250000) X1 = p1.rvs(n_samples=250000, random_state=random_state) X = np.vstack((X0, X1)) y = np.zeros(len(X)) y[len(X0):] = 1 ratio.fit(X, y) # Evaluate log-likelihood ratio r = ratio.predict(X_true, log=True) value = -np.mean(r[np.isfinite(r)]) # optimization is more stable using mean # this will need to be rescaled by len(X_true) return value
from GPyOpt.methods import BayesianOptimization bounds = [(-3, 3), (-3, 3)] solver = BayesianOptimization(vectorize(objective), bounds) solver.run_optimization(max_iter=50, true_gradients=False)
approx_MLE = solver.x_opt print("Approx. MLE =", approx_MLE)
Approx. MLE = [ 1.01455539 -0.90202743]
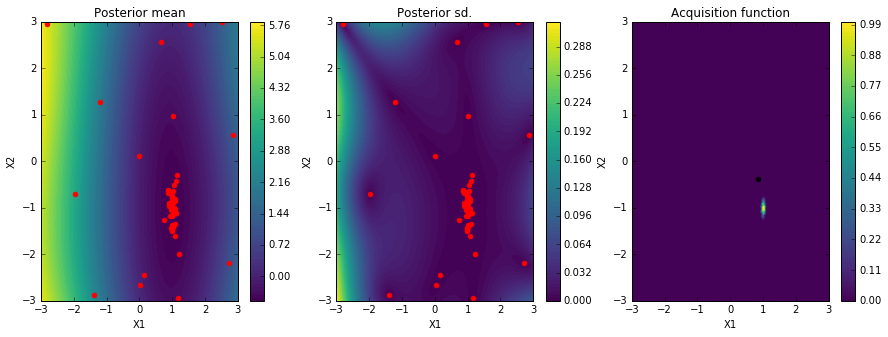
solver.plot_acquisition()
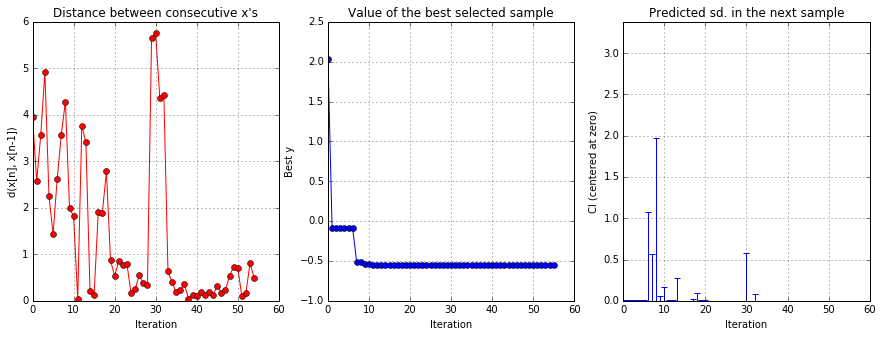
solver.plot_convergence()
# Minimize the surrogate GP approximate of the approximate LR def gp_objective(theta): theta = theta.reshape(1, -1) return solver.model.predict(theta)[0][0] r = minimize(gp_objective, x0=[0, 0]) gp_MLE = r.x print("GP MLE =", gp_MLE)
GP MLE = [ 1.00846361 -1.00438228]
Here we plot the posterior mean of the Gaussian Process surrogate learned by the Bayesian Optimization algorithm.
# Plot GP contours A.set_value(true_A) B.set_value(true_B) bounds = [(exact_MLE[0] - 0.16, exact_MLE[0] + 0.16), (exact_MLE[1] - 0.5, exact_MLE[1] + 0.5)] As = np.linspace(*bounds[0], 100) Bs = np.linspace(*bounds[1], 100) AA, BB = np.meshgrid(As, Bs) X = np.hstack((AA.reshape(-1, 1), BB.reshape(-1, 1)))
from scipy.stats import chi2 gp_contours, _= solver.model.predict(X) gp_contours = 2. * (gp_contours - r.fun) * len(X_true) # Rescale cs = plt.contour(As, Bs, gp_contours.reshape(AA.shape), levels=[chi2.ppf(0.683, df=2), chi2.ppf(0.9545, df=2), chi2.ppf(0.9973, df=2)], colors=["w"]) plt.contourf(As, Bs, gp_contours.reshape(AA.shape), 50, vmin=0, vmax=30) cb = plt.colorbar() plt.plot(solver.X[:, 0], solver.X[:, 1], 'w.', markersize=8) plt.plot([true_A], [true_B], "r.", markersize=8) plt.plot([exact_MLE[0]], [exact_MLE[1]], "g.", markersize=8) plt.plot([gp_MLE[0]], [gp_MLE[1]], "b.", markersize=8) plt.axis((*bounds[0], *bounds[1])) plt.xlabel(r"$\alpha$") plt.ylabel(r"$\beta$") #plt.savefig("fig4b.pdf") plt.show()
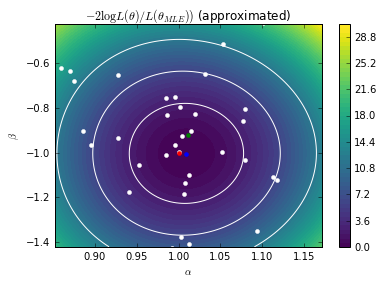
Finally, we plot the approximate likelihood from a grid scan. Statistical fluctuations in the calibration lead to some noise in the scan. The Gaussian Process surrogate above smooths out this noise providing a smoother approximate likelihood.
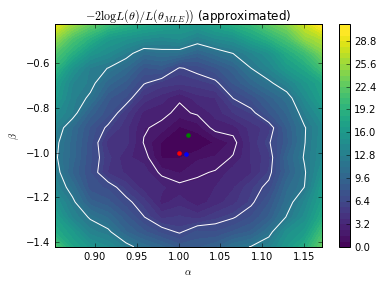
# Contours of the approximated LR A.set_value(true_A) B.set_value(true_B) bounds = [(exact_MLE[0] - 0.16, exact_MLE[0] + 0.16), (exact_MLE[1] - 0.5, exact_MLE[1] + 0.5)] As = np.linspace(*bounds[0], 16) Bs = np.linspace(*bounds[1], 16) AA, BB = np.meshgrid(As, Bs) X = np.hstack((AA.reshape(-1, 1), BB.reshape(-1, 1)))
approx_contours = np.zeros(len(X)) i = 0 for a in As: for b in Bs: approx_contours[i] = objective([a, b]) i += 1 approx_contours = 2. * (approx_contours - approx_contours.min()) * len(X_true)
plt.contour(As, Bs, approx_contours.reshape(AA.shape).T, levels=[chi2.ppf(0.683, df=2), chi2.ppf(0.9545, df=2), chi2.ppf(0.9973, df=2)], colors=["w"]) plt.contourf(As, Bs, approx_contours.reshape(AA.shape).T, 50, vmin=0, vmax=30) plt.colorbar() plt.plot([true_A], [true_B], "r.", markersize=8) plt.plot([exact_MLE[0]], [exact_MLE[1]], "g.", markersize=8) plt.plot([gp_MLE[0]], [gp_MLE[1]], "b.", markersize=8) plt.axis((*bounds[0], *bounds[1])) plt.xlabel(r"$\alpha$") plt.ylabel(r"$\beta$") #plt.savefig("fig4c.pdf") plt.show()
 Top
Top