Diagnostics for approximate likelihood ratios
Kyle Cranmer, Juan Pavez, Gilles Louppe, March 2016.
This is an extension of the example in Parameterized inference from multidimensional data. To aid in visualization, we restrict to a 1-dimensional slice of the likelihood along $\alpha$ with $\beta=-1$. We consider three situations: i) a poorly trained, but well calibrated classifier; ii) a well trained, but poorly calibrated classifier; and iii) a well trained, and well calibrated classifier. For each case, we employ two diagnostic tests. The first checks for independence of $-2\log\Lambda(\theta)$ with respect to changes in the reference value $\theta_1$. The second uses a classifier to distinguish between samples from $p(\mathbf{x}|\theta_0)$ and samples from $p(\mathbf{x}|\theta_1)$ weighted according to $r(\mathbf{x}; \theta_0, \theta_1)$.
%matplotlib inline import matplotlib.pyplot as plt import numpy as np import theano from scipy.stats import chi2 from itertools import product np.random.seed(314)
Create model and generate artificial data
from carl.distributions import Join from carl.distributions import Mixture from carl.distributions import Normal from carl.distributions import Exponential from carl.distributions import LinearTransform from sklearn.datasets import make_sparse_spd_matrix # Parameters true_A = 1. A = theano.shared(true_A, name="A") # Build simulator R = make_sparse_spd_matrix(5, alpha=0.5, random_state=7) p0 = LinearTransform(Join(components=[ Normal(mu=A, sigma=1), Normal(mu=-1, sigma=3), Mixture(components=[Normal(mu=-2, sigma=1), Normal(mu=2, sigma=0.5)]), Exponential(inverse_scale=3.0), Exponential(inverse_scale=0.5)]), R) # Define p1 at fixed arbitrary value A=0 p1s = [] p1_params = [(0,-1),(1,-1),(0,1)] for p1_p in p1_params: p1s.append(LinearTransform(Join(components=[ Normal(mu=p1_p[0], sigma=1), Normal(mu=p1_p[1], sigma=3), Mixture(components=[Normal(mu=-2, sigma=1), Normal(mu=2, sigma=0.5)]), Exponential(inverse_scale=3.0), Exponential(inverse_scale=0.5)]), R)) p1 = p1s[0] # Draw data X_true = p0.rvs(500, random_state=314)
Known likelihood setup
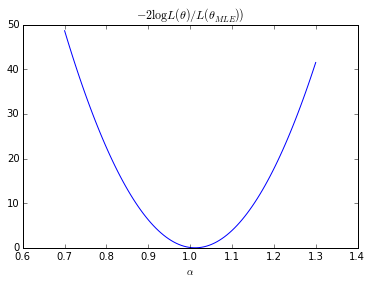
# Minimize the exact LR from scipy.optimize import minimize p1 = p1s[2] def nll_exact(theta, X): A.set_value(theta[0]) return (p0.nll(X) - p1.nll(X)).sum() r = minimize(nll_exact, x0=[0], args=(X_true,)) exact_MLE = r.x print("Exact MLE =", exact_MLE)
('Exact MLE =', array([ 1.01185166]))
# Exact LR A.set_value(true_A) nlls = [] As_ = [] bounds = [(true_A - 0.30, true_A + 0.30)] As = np.linspace(bounds[0][0],bounds[0][1], 100) nll = [nll_exact([a], X_true) for a in As] nll = np.array(nll) nll = 2. * (nll - r.fun)
plt.plot(As, nll) plt.xlabel(r"$\alpha$") plt.title(r"$-2 \log L(\theta) / L(\theta_{MLE}))$") plt.show()
Likelihood-free setup
Here we create the data to train a parametrized classifier
# Build classification data from carl.learning import make_parameterized_classification bounds = [(-3, 3), (-3, 3)] clf_parameters = [(1000, 100000), (1000000, 500), (1000000, 100000)] X = [0]*3*3 y = [0]*3*3 for k,(param,p1) in enumerate(product(clf_parameters,p1s)): X[k], y[k] = make_parameterized_classification( p0, p1, param[0], [(A, np.linspace(bounds[0][0],bounds[0][1], num=30))], random_state=0)
# Train parameterized classifier from carl.learning import as_classifier from carl.learning import make_parameterized_classification from carl.learning import ParameterizedClassifier from sklearn.neural_network import MLPRegressor from sklearn.pipeline import make_pipeline from sklearn.preprocessing import StandardScaler clfs = [] for k, _ in enumerate(product(clf_parameters,p1s)): clfs.append(ParameterizedClassifier( make_pipeline(StandardScaler(), as_classifier(MLPRegressor(learning_rate="adaptive", hidden_layer_sizes=(40, 40), tol=1e-6, random_state=0))), [A])) clfs[k].fit(X[k], y[k])
from carl.learning import CalibratedClassifierCV from carl.ratios import ClassifierRatio def vectorize(func,n_samples,clf,p1): def wrapper(X): v = np.zeros(len(X)) for i, x_i in enumerate(X): v[i] = func(x_i,n_samples=n_samples,clf=clf, p1=p1) return v.reshape(-1, 1) return wrapper def objective(theta, random_state=0, n_samples=100000, clf=clfs[0],p1=p1s[0]): # Set parameter values A.set_value(theta[0]) # Fit ratio ratio = ClassifierRatio(CalibratedClassifierCV( base_estimator=clf, cv="prefit", # keep the pre-trained classifier method="histogram", bins=50)) X0 = p0.rvs(n_samples=n_samples) X1 = p1.rvs(n_samples=n_samples, random_state=random_state) X = np.vstack((X0, X1)) y = np.zeros(len(X)) y[len(X0):] = 1 ratio.fit(X, y) # Evaluate log-likelihood ratio r = ratio.predict(X_true, log=True) value = -np.mean(r[np.isfinite(r)]) # optimization is more stable using mean # this will need to be rescaled by len(X_true) return value
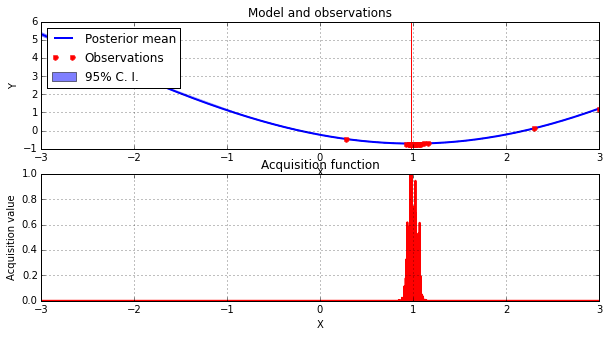
Now we use a Bayesian optimization procedure to create a smooth surrogate of the approximate likelihood.
from GPyOpt.methods import BayesianOptimization solvers = [] for k, (param, p1) in enumerate(product(clf_parameters,p1s)): clf = clfs[k] n_samples = param[1] bounds = [(-3, 3)] solvers.append(BayesianOptimization(vectorize(objective,n_samples,clf,p1), bounds)) solvers[k].run_optimization(max_iter=50, true_gradients=False)
approx_MLEs = [] for k, _ in enumerate(product(clf_parameters,p1s)): solver = solvers[k] approx_MLE = solver.x_opt approx_MLEs.append(approx_MLE) print("Approx. MLE =", approx_MLE)
('Approx. MLE =', array([ 1.1567223]))
('Approx. MLE =', array([ 1.12968218]))
('Approx. MLE =', array([ 1.27133084]))
('Approx. MLE =', array([ 1.09549403]))
('Approx. MLE =', array([ 0.91981054]))
('Approx. MLE =', array([ 0.77314181]))
('Approx. MLE =', array([ 1.02540673]))
('Approx. MLE =', array([ 1.00016057]))
('Approx. MLE =', array([ 1.0148428]))
solver.plot_acquisition()
solver.plot_convergence()
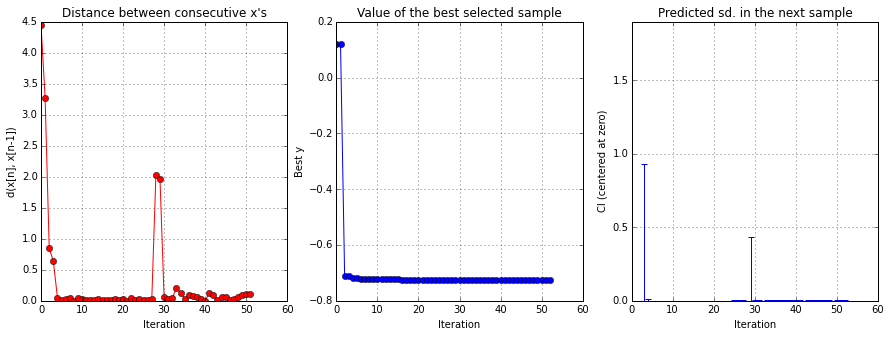
# Minimize the surrogate GP approximate of the approximate LR rs = [] solver = solvers[0] for k, _ in enumerate(product(clf_parameters,p1s)): def gp_objective(theta): theta = theta.reshape(1, -1) return solvers[k].model.predict(theta)[0][0] r = minimize(gp_objective, x0=[0]) rs.append(r) gp_MLE = r.x print("GP MLE =", gp_MLE)
('GP MLE =', array([ 1.15409679]))
('GP MLE =', array([ 1.13815972]))
('GP MLE =', array([ 1.25892465]))
('GP MLE =', array([ 1.03389187]))
('GP MLE =', array([ 0.93057811]))
('GP MLE =', array([ 0.7587189]))
('GP MLE =', array([ 1.01290299]))
('GP MLE =', array([ 1.00689144]))
('GP MLE =', array([ 0.99879448]))
#bounds = [(exact_MLE[0] - 0.16, exact_MLE[0] + 0.16)] approx_ratios = [] gp_ratios = [] gp_std = [] gp_q1 = [] gp_q2 = [] n_points = 30 for k,(param,p1) in enumerate(product(clf_parameters,p1s)): clf = clfs[k] n_samples = param[1] solver = solvers[k] #As = np.linspace(*bounds[0], 100) nll_gp, var_gp = solvers[k].model.predict(As.reshape(-1, 1)) nll_gp = 2. * (nll_gp - rs[k].fun) * len(X_true) gp_ratios.append(nll_gp) # STD std_gp = np.sqrt(4*var_gp*len(X_true)*len(X_true)) std_gp[np.isnan(std_gp)] = 0. gp_std.append(std_gp) # 95% CI q1_gp, q2_gp = solvers[k].model.predict_quantiles(As.reshape(-1, 1)) q1_gp = 2. * (q1_gp - rs[k].fun) * len(X_true) q2_gp = 2. * (q2_gp - rs[k].fun) * len(X_true) gp_q1.append(q1_gp) gp_q2.append(q2_gp)
Plots for the first diagonstic: $\theta_1$-independence
bounds = [(true_A - 0.30, true_A + 0.30)] for k, _ in enumerate(clf_parameters): fig = plt.figure() ax = fig.add_subplot(1,1,1) ax.plot(As, nll, label="Exact") #plt.plot(np.linspace(*bounds[0], n_points), nll_approx - , label="approx.") #plt.plot(np.linspace(bounds[0][0],bounds[0][1], n_points), nll_approx , label="approx.") ax.plot(As, gp_ratios[3*k], label=r"Approx., $\theta_1=(\alpha=0,\beta=-1)$") ax.plot(As, gp_ratios[3*k+1], label=r"Approx., $\theta_1=(\alpha=1,\beta=-1)$") ax.fill_between(As,(gp_ratios[3*k] - gp_std[3*k]).ravel(),(gp_ratios[3*k] + gp_std[3*k]).ravel(), color='g',alpha=0.2) ax.plot(As, gp_ratios[3*k+2], label=r"Approx., $\theta_1=(\alpha=0,\beta=1)$") handles, labels = ax.get_legend_handles_labels() ax.set_xlabel(r"$\alpha$") ax.set_ylabel(r"$-2 \log \Lambda(\theta)$") #plt.legend() p5 = plt.Rectangle((0, 0), 0.2, 0.2, fc="green",alpha=0.2,edgecolor='none') handles.insert(4,p5) labels.insert(4,r"$\pm 1 \sigma$, $\theta_1=(\alpha=0,\beta=-1)$") handles[1],handles[-2] = handles[-2],handles[1] labels[1],labels[-2] = labels[-2],labels[1] ax.legend(handles,labels) ax.set_ylim(0, 14) ax.set_xlim(bounds[0][0],bounds[0][1]) plt.savefig('likelihood_comp_{0}.pdf'.format(k)) plt.show()
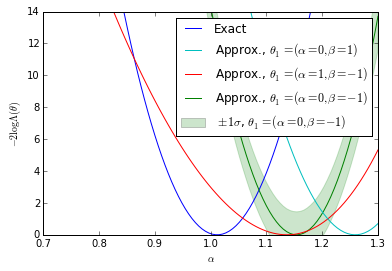
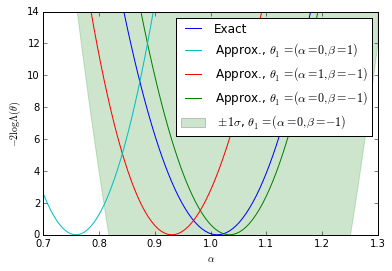
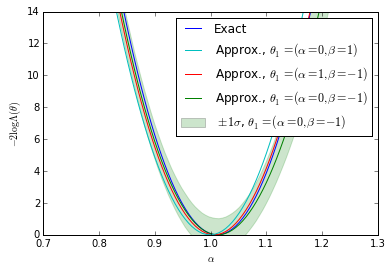
We show the posterior mean of a Gaussian processes resulting from Bayesian optimization of the raw approximate likelihood. In addition, the standard deviation of the Gaussian process is shown for one of the $\theta_1$ reference points to indicate the size of these statistical fluctuations. It is clear that in the well calibrated cases that these fluctuations are small, while in the poorly calibrated case these fluctuations are large. Moreover, in the first case we see that in the poorly trained, well calibrated case the classifier $\hat{s}(\mathbf{x}; \theta_0, \theta_1)$ has a significant dependence on the $\theta_1$ reference point. In contrast, in the second case the likelihood curves vary significantly, but this is comparable to the fluctuations expected from the calibration procedure. Finally, the third case shows that in the well trained, well calibrated case that the likelihood curves are all consistent with the exact likelihood within the estimated uncertainty band of the Gaussian process.
The second diagnostic - ROC curves for a discriminator
from sklearn.metrics import roc_curve, auc def makeROC(predictions ,targetdata): fpr, tpr, _ = roc_curve(targetdata.ravel(),predictions.ravel()) roc_auc = auc(fpr, tpr) return fpr,tpr,roc_auc
# I obtain data from r*p1 by resampling data from p1 using r as weights def weight_data(x0,x1,weights): x1_len = x1.shape[0] weights = weights / weights.sum() weighted_data = np.random.choice(range(x1_len), x1_len, p = weights) w_x1 = x1.copy()[weighted_data] y = np.zeros(x1_len * 2) x_all = np.vstack((w_x1,x0)) y_all = np.zeros(x1_len * 2) y_all[x1_len:] = 1 return (x_all,y_all) p1 = p1s[0] X0_roc = p0.rvs(500000,random_state=777) X1_roc = p1.rvs(500000,random_state=777) # Roc curve comparison for p0 - r*p1 for k,param in enumerate(clf_parameters): #fig.add_subplot(3,2,(k+1)*2) clf = clfs[3*k] n_samples = param[1] X0 = p0.rvs(n_samples) X1 = p1.rvs(n_samples,random_state=777) X_len = X1.shape[0] ratio = ClassifierRatio(CalibratedClassifierCV( base_estimator=clf, cv="prefit", # keep the pre-trained classifier method="histogram", bins=50)) X = np.vstack((X0, X1)) y = np.zeros(len(X)) y[len(X0):] = 1 ratio.fit(X, y) # Weighted with true ratios true_r = p0.pdf(X1_roc) / p1.pdf(X1_roc) true_r[np.isinf(true_r)] = 0. true_weighted = weight_data(X0_roc,X1_roc,true_r) # Weighted with approximated ratios app_r = ratio.predict(X1_roc,log=False) app_r[np.isinf(app_r)] = 0. app_weighted = weight_data(X0_roc,X1_roc,app_r) clf_true = MLPRegressor(tol=1e-05, activation="logistic", hidden_layer_sizes=(10, 10), learning_rate_init=1e-07, learning_rate="constant", algorithm="l-bfgs", random_state=1, max_iter=75) clf_true.fit(true_weighted[0],true_weighted[1]) predicted_true = clf_true.predict(true_weighted[0]) fpr_t,tpr_t,roc_auc_t = makeROC(predicted_true, true_weighted[1]) plt.plot(fpr_t, tpr_t, label=r"$p(x|\theta_1)r(x|\theta_0,\theta_1)$ exact" % roc_auc_t) clf_true.fit(np.vstack((X0_roc,X1_roc)),true_weighted[1]) predicted_true = clf_true.predict(np.vstack((X0_roc,X1_roc))) fpr_f,tpr_f,roc_auc_f = makeROC(predicted_true, true_weighted[1]) plt.plot(fpr_f, tpr_f, label=r"$p(x|\theta_1)$ no weights" % roc_auc_f) clf_true.fit(app_weighted[0],app_weighted[1]) predicted_true = clf_true.predict(app_weighted[0]) fpr_a,tpr_a,roc_auc_a = makeROC(predicted_true, app_weighted[1]) plt.plot(fpr_a, tpr_a, label=r"$p(x|\theta_1)r(x|\theta_0,\theta_1)$ approx." % roc_auc_a) plt.plot([0, 1], [0, 1], 'k--') plt.xlim([0.0, 1.0]) plt.ylim([0.0, 1.05]) plt.xlabel('False Positive Rate') plt.ylabel('True Positive Rate') plt.legend(loc="lower right") plt.tight_layout() plt.savefig('ROC_comp{0}.pdf'.format(k)) plt.show() #plt.tight_layout() #plt.savefig('all_comp.pdf'.format(k))

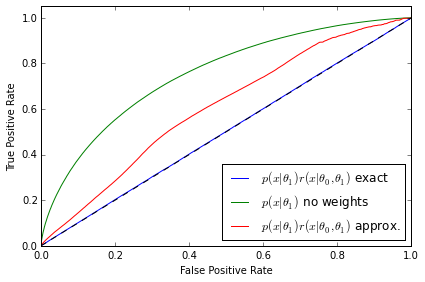
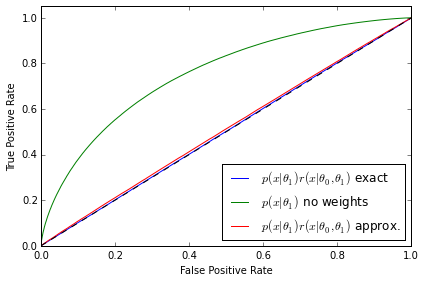
The ROC curves tell a similarly revealing story. As expected, the classifier is not able to distinguish between the distributions when $p(\mathbf{x}|\theta_1)$ is weighted by the exact likelihood ratio. We can also rule out that this is a deficiency in the classifier because the two distributions are well separated when no weights are applied to $p(\mathbf{x}|\theta_1)$. In both the first and second examples the ROC curve correctly diagnoses deficiencies in the approximate likelihood ratio $\hat{r}(\hat{s}(\mathbf{x}; \theta_0, \theta_1))$. Finally, third example shows that the ROC curve in the well trained, well calibrated case is almost identical with the exact likelihood ratio, confirming the quality of the approximation.
 Top
Top